Gerak muter

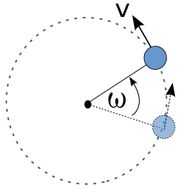
Gerak muter.

Gerak muter nyaéta gerak hiji barang anu nyieun jalur liliwatan mangrupa bunderan nu ngalingkung hiji titik nu tetep. Ambéh hiji barang bisa gerak muter, ieu barang merlukeun ayana gaya anu bakal mengkolkeun barang kasebut nuju ka puseur bunderan. Gaya ieu dingaranan gaya séntripétal. Hiji gerak muter beraturan (merenah) bisa disebut ogé gerak digancangkeun merenah, lantaran perlu ayana hiji pacepetan (akselerasi) anu gedéna tetep kalayan tujuan anu robah, anu ngabalukarkeun robahna tujuan gerak hiji barang ambéh ngaliwatan jalur anu ngawangun bunderan Richard S. Westfall, Circular Motion in Seventeenth-century Mechanics, Isis, Vol. 63, No. 2. (Jun., 1972), pp. 184-189..

Diménsi pikeun gerak muter

Diménsi-diménsi anu ngagambarkeun hiji gerak muter nyaéta sudut, laju sudut sarta akselerasi sudut anu masing-masing dilambangkeun ku $\theta\!$, $\omega\!$ sarta $\alpha\!$. Diménsi-diménsi ieu lamun dianalogikan jeung gerak liniér sarimbag jeung posisi, laju sarta akselerasi anu masing-masing dilambangkeun ku $r\!$, $v\!$ sarta $a\!$.

Diménsi gerak lempeng jeung gerak muter

Gerak lempeng		Gerak muter
Diménsi	Hijian (SI)	Diménsi	Hijian (SI)
poisisi $r\!$	m	sudut $\theta\!$	rad
laju $v\!$	m/s	laju sudut $\omega\!$	rad/s
akselerasi $a\!$	m/s2	akselerasi sudut $\alpha\!$	rad/s2
-	-	perioda $T\!$	s
-	-	radius $R\!$	m

Diférensiasi jeung integrasi

Diménsi-diménsi gerak muter ngabogaan hubungan dina prosés integrasi jeung diférensiasi.

$\int \omega\ dt = \theta \ \ \leftrightarrow\ \ \omega = \frac{d\theta}{dt}$

$\int \alpha\ dt = \omega \ \ \leftrightarrow\ \ \alpha = \frac{d\omega}{dt}$

$\int \int \alpha\ dt^2 = \theta \ \ \leftrightarrow\ \ \alpha = \frac{d^2\theta}{dt^2}$

Hubungan antara diménsi sudut jeung tangénsial

Antara diménsi gerak liniér jeung gerak muter aya hiji hubungan ngaliwatan $R\!$ husus pikeun komponén tangénsial, nyaéta

$\theta = \frac{r_T}{R}\ \ , \ \ \omega = \frac{v_T}{R}\ \ , \ \ \alpha = \frac{a_T}{R}$

Perhatikeun yén di dieu dipaké $r_T\!$ anu didéfinisikan sabagé jarak anu diliwatan atawa sisi gondéwa anu geus diliwatan salila hiji selang waktu sarta lain ngan posisi dina hiji waktu, nyaéta

$r_T \approx|\overrightarrow{r}(t+\Delta t)-\overrightarrow{r}(t)|\!$

pikeun hiji selang waktu singket atawa sudut anu heureut.

Rupa-rupa gerak muter

Gerak muter bisa dibédakeun jadi dua rupa dumasar kana kasarageman laju sudutna $\omega\!$, nyaéta:

• gerak muter beraturan (merenah), sarta
• gerak muter robah beraturan (merenah).

Gerak muter merenah

Gerak muter merenah nyaéta gerak muter kalawan laju sudut $\omega\!$ nu tetep. Harga laju sudut bisa dibeunangkeun ku cara ngabagi laju tangénsial $v_T\!$ ku radius puteran $R\!$

$\omega = \frac {v_t} R$

Arah tujuan laju liniér $v\!$ dina gerak muter merenah sok nyigeung jalur liliwatan, anu hartina arah tujuanana sarua jeung arah tujuan laju tangénsial $v_T\!$. Tetepna harga laju $v_T\!$ alatan tina tetepna harga $\omega\!$. Sajaba ti éta, aya ogé akselerasi radial $a_R\!$ anu hargana tetep sarta arah tujuanana anu robah. Akselerasi ieu disebut akselerasi séntripétal, di mana arah tujuanana sok ngarah puseur bunderan.

$a_R = \frac {v^2} R = \frac {v_t^2} R$

Lamun $T\!$ nyaéta waktu anu diperlukeun pikeun ngabéréskeun hiji puteran sapinuhna dina jalur bunderan $\theta = 2\pi R\!$, mangka bisa ogé dituliskeun

$v_T = \frac {2\pi R} T \!$

Kinematika gerak muter beraturan nyaéta

$\theta(t) = \theta_0 + \omega\ t$

dimana $\theta(t)\!$ mangrupakeun sudut anu diliwatan salila hiji waktu $t\!$, $\theta_0\!$ mangrupakeun sudut awal sarta \omega\! mangrupakeun laju sudut (anu tetep hargana).

Gerak muter robah merenah

Gerak muter robah merenah nyaéta gerak muter kalawan laju sudut $\alpha\!$ nu tetep. Dina gerak ieu aya akselerasi tangensial $a_T\!$ (anu dina hal ieu sarua jeung akselerasi liniér) anu nyigeung jalur kuliling bunderan (pahapit jeung arah tujuan laju tangénsial $v_T\!$).

$\alpha = \frac {a_t} R$

Kinematika GMBB nyaéta

$\omega(t) = \omega_0 + \alpha\ t \!$

$\theta(t) = \theta_0 + \omega_0\ t + \frac12 \alpha\ t^2 \!$

$\omega^2(t) = \omega_0^2 + 2 \alpha\ (\theta(t) - \theta_0) \!$

dimana $\alpha\!$ nyaéta akselerasi sudut anu hargana tetep sarta $\omega_0\!$ nyaéta laju sudut awal.

Persamaan paramétrik

Gerak muter bisa ogé dinyatakeun dina persamaan paramétrik kalawan leuwih tiheula ngadéfinisikeun:

• titik mimiti gerak dipigawé $(x_0,y_0)\!$
• laju sudut puteran $\omega\!$ (anu hartina hiji GMB)
• puseur bunderan $(x_c,y_c)\!$

pikeun saterusna dijieun persamaanna Chapter 22 Parametric Equation,, Department of Mathematics, University of Washington, Math 124 Materials (Autumn), ch 22, pp. 308..

Hal kahiji anu kudu dipigawé nyaéta ngitung radius liliwatan $R\!$ :

$R = \sqrt{(x_0 - x_c)^2 + (y_0 - y_c)^2} \!$

Sanggeus meunang harga radius liliwatan, persamaan bisa dituliskeun:

$x(t) = x_c + R cos(\omega t + \phi_x) \!$

$y(t) = y_c + R sin(\omega t + \phi_y) \!$

jeung dua konstanta $\phi_x \!$ sarta $\phi_y \!$ anu masih kudu ditangtukeun hargana. Kalawan pasaratan saméméhna, nyaéta dipikanyahona harga $(x_0,y_0)\!$, mangka bisa ditangtukeun harga $\phi_x \!$ sarta $\phi_y \!$:

$\phi_x = \arccos \left( \frac{x_0 - x_c}{R} \right)\!$

$\phi_y = \arcsin \left( \frac{y_0 - y_c}{R} \right)\!$

Perlu dipikanyaho yén sabenerna

$\phi_x = \phi_y \!$

alatan mangrupa sudut mimiti gerak muter.

Hubungan antar diménsi liniér jeung angular

Ku ngagunakeun persamaan paramétrik, geus diwatesan yén diménsi liniér anu dipaké saukur diménsi tangensial atawa ngan komponén véktor dina arah tujuan sudut, anu hartina euweuh komponén véktor dina arah tujuan radial. Ku watesan ieu, hubungan antara diménsi liniér (tangensial) sarta sudut bisa kalawan gampang ditimukeun.

Laju tangensial sarta laju sudut

Laju liniér total bisa katimu ngaliwatan persamaan:

$v = \sqrt{v_x^2 + v_y^2}$

sarta alatan watesan impleméntasi persamaan paramétrik dina gerak muter, mangka

$v_T = v = \sqrt{v_x^2 + v_y^2}$

kalawan

$v_x = \dot{x} = \frac{dx}{dt}$

$v_y = \dot{y} = \frac{dy}{dt}$

dihasilkeun

$v_x = -\omega R \sin(\omega t + \phi_x) \!$

$v_y = \omega R \cos(\omega t + \phi_x) \!$

ku kituna

$v_T = \sqrt{(-\omega)^2 R^2 \sin^2(\omega t + \phi_x) + \omega^2 R^2 \cos^2(\omega t + \phi_x)}\!$

$v_T = \omega R \sqrt{\sin^2(\omega t + \phi_x) + \cos^2(\omega t + \phi_x)}\!$

$v_T = \omega R\!$

Akselerasi tangensial jeung laju sudut

Ku cara anu sarua jeung nu saméméhna, akselerasi liniér total bisa katimu ngaliwatan persamaan:

$a = \sqrt{a_x^2 + a_y^2}$

sarta alatan watesan impleméntasi persamaan paramétrik dina gerak muter, mangka

$a_T = a = \sqrt{a_x^2 + a_y^2}$

kalawan

$a_x = \ddot{x} = \frac{d^2x}{dt^2}$

$a_y = \ddot{y} = \frac{d^2y}{dt^2}$

dihasilkeun

$a_x = -\omega^2 R \cos(\omega t + \phi_x) \!$

$a_y = -\omega^2 R \sin(\omega t + \phi_x) \!$

ku kituna

$a_T = \sqrt{(-\omega)^4 R^2 \cos^2(\omega t + \phi_x) + \omega^4 R^2 \sin^2(\omega t + \phi_x)}\!$

$a_T = \omega^2 R \sqrt{\cos^2(\omega t + \phi_x) + \sin^2(\omega t + \phi_x)}\!$

$a_T = \omega^2 R\!$

Laju sudut henteu tetep

Persamaan paramétrik bisa ogé dipaké lamun gerak muter GMBB, atawa lain deui GMB kalawan ayana laju sudut anu robah merenah (atawa ayana akselerasi). Léngkah-léngkah anu sarua bisa dipigawé di dieu, tapi perlu diinget yén

$\omega \rightarrow \omega(t) = \int \alpha dt = \omega_0 + \alpha t \!$

kalawan $\alpha\!$ laju sudut sarta $\omega_0\!$ laju sudut awal. Penurunan GMBB ieu baris jadi saeutik leuwih rumit dibandingkeun dina kasus GMB di luhur.

Persamaan paramétrik di luhur, bisa dituliskeun dina wangun anu leuwih umum, nyaéta:

$x(t) = x_c + R \cos \theta \!$

$y(t) = y_c + R \sin \theta \!$

di mana $\theta = \theta(t) \!$ nyaéta sudut anu diliwatan dina hiji waktu. Kawas geus disebutkeun di luhur ngeunaan hubungan antara $\theta \!$, $\omega \!$ jeung $\alpha \!$ ngaliwatan prosés integrasi sarta diférensiasi, mangka dina kasus GMBB hubungan-hubungan kasebut mutlak diperlukeun.

Laju sudut

Ku ngagunakeun aturan ranté dina ngalakonan diférensiasi posisi ti persamaan paramétrik katimu:

$v_x(t) = - R \sin \theta\ \frac{d\theta}{dt} = - \omega(t) R \sin \theta \!$

$v_y(t) = R \cos \theta \ \frac{d\theta}{dt} = \omega(t) R \cos \theta \!$

kalawan

$\frac{d\theta}{dt} = \omega(t) = \omega_0 + \alpha\ t \!$

Bisa dibuktikeun yén

$v(t) = v_t(t) = \sqrt{v_x^2(t) + v_y^2(t)} = \omega(t) R \!$

sarua jeung kasus dina GMB.

Akselerasi total

Diférensiasi laju liniér dumasar waktu satuluyna ngahasilkeun

$a_x(t) = - R \cos \theta \ \left( \frac{d\theta}{dt} \right)^2 - R \sin \theta \frac{d^2\theta}{dt^2} \!$

$a_x(t) = - R \sin \theta \ \left( \frac{d\theta}{dt} \right)^2 + R \cos\theta \frac{d^2\theta}{dt^2} \!$

anu bisa disederhanakan jadi

$a_x(t) = - \omega^2 R \cos \theta - \alpha R \sin \theta \!$

$a_x(t) = - \omega^2 R \sin \theta + \alpha R \cos \theta \!$

Saterusna

$a^2(t) = a_x^2(t) + a_y^2(t) = R^2\left(\omega^4(t) + \alpha^2 \right) \!$

anu umumna dituliskeun Ian Burley, Meg Carrington, Randy Kobes, Gabor Kunstatter, Centripetal Acceleration, IUN/FYDE Introductory Physics Notes, circ:node6, University of Winnipeg, 10/9/1997.

$a^2(t) = a_r^2(t) + a_t^2(t) \!$

kalawan

$a_T = \alpha R \!$

anu mangrupa akselerasi sudut, sarta

$a_R = \omega^2 R = a_s \!$

anu mangrupa akselerasi séntripétal. Sélér séntripétal ieu mecenghul alatan obyék kudu dipéngkolkeun atawa lajuna kudu dirobah ku kituna gerak nuturkeun liliwatan bunderan.

Gerak robah merenah

Gerak muter bisa ditoong minangka gerak robah merenah. Bédakeun jeung gerak lempeng robah merenah (GLBB). Konsép laju anu robah sakapeung ngan dipahaman dina robahan badagna, dina gerak muter merenah (GMB) gedéna laju nyaéta tetep, tapi arah tujuanana anu robah sacara merenah, bandingkeun jeung GLBB anu arah tujuanana tetep tapi gedé lajuna anu robah merenah.

Gerak robah merenah

LAju	GLBB	GMB
Gedé	robah	tetep
Arah tujuan	tetep	robah