Fungsi Singularitas

Fungsi singularitas nyaéta hiji notasi (perlambang) anu digunakeun pikeun ngagambarkeun fungsi-fungsi anu henteu kontinyu. Salah sahiji bentuk sinyal non périodik anu penting dina téori telekomunikasi nyaéta fungsi singularitas.

Fungsi tangga hijian.

Fungsi tangga hijian

Fungsi tangga hijian u(t) didéfinisikeun salaku:

$u(t) = \begin{cases} 1 & t > 0 \\ 0 & t < 0 \end{cases}$

Fungsi impuls hijian

Fungsi impuls hijian.

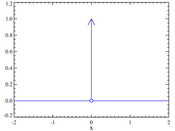
Fungsi impuls hijian, anu dipikawanoh ogé salaku fungsi délta Dirac, δ(t) lain mangrupakeun fungsi nu biasa sarta didéfinisikeun ku cara saperti kieu:

$\delta(t) = \begin{cases} \infty, & t = 0 \\ 0, & t \ne 0 \end{cases}$

atawa:

$\int_{-\infty}^{\infty}\phi(t)\delta(t)\mathrm{d}t = \phi(0)$

Derivasi fungsi-fungsi singularitas

Lamun g(t) mangrupakeun fungsi singularitas, derivasi tina éta fungsi, nyaéta g'(t) didéfinisikeun salaku:

$\int_{-\infty}^{\infty} g'(t)\phi(t)\mathrm{d}t = - \int_{-\infty}^{\infty} g(t)\phi'(t)\mathrm{d}t$

dimana phi'(t) mangrupakeun derivasi ti phi(t).

Persamaan kasebut di luhur sarua jeung:

$\phi(t) = u'(t) = \frac{\mathrm d u(t)}{\mathrm d t}$

Tempo ogé

• [Macaulay brackets]

Rujukan

1. Hwei P. Hsu, Ph.D, Theory and Problems of Analogue and Digital Communications, Schaum's Outline, McGraw-Hill, 1993

Artikel ieu mangrupa taratas, perlu disampurnakeun. Upami sadérék uninga langkung paos perkawis ieu, dihaturan kanggo ngalengkepan.