Konvolusi

Dina matematika sarta, hususna, analisis fungsional, konvolusi nyaéta operator matematis anu ngajadikeun dua fungsi x1 jeung x2 jadi fungsi katilu nu dianggap salaku vérsi modifikasi tina fungsi-fungsi asal. Konvolusi mangrupa hiji alat matematika dina élmu statistik, citra, pamrosésan sinyal, sarta persamaan diférential.

Gambaran visual ngeunaan konvolusi.

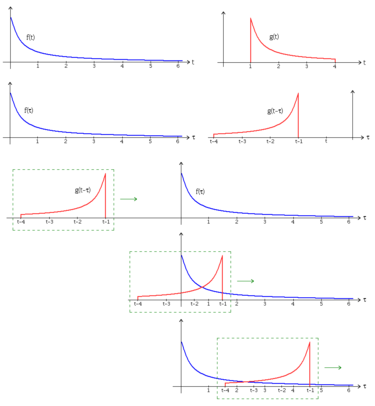
Définisi

Konvolusi tina dua sinyal $x_{1}(t)$ jeung $x_{2}(t)$, nu dilambangkeun ku $x_{1}(t)*x_{2}(t)$ nyaéta hiji sinyal anyar x(t) anu didéfinisikeun ku:

$x(t)=x_{1}(t)*x_{2}(t)=(x_{1}*x_{2})(t)=\int _{-\infty }^{\infty }x_{1}(\tau )x_{2}(t-\tau )\,d\tau .$

Sifat konvolusi

$x_{1}(t)*x_{2}(t)=x_{2}(t)*x_{1}(t)\,$

$x_{1}(t)*[x_{2}(t)*x_{3}(t)]=[x_{1}(t)*x_{2}(t)]*x_{3}(t)\,$

$x_{1}(t)*[x_{2}(t)+x_{3}(t)]=[x_{1}(t)*x_{2}(t)]+[x_{1}(t)*x_{3}(t)]\,$

Konvolusi jeung fungsi $\delta$

$x_{1}(t)*\delta (t)=\delta (t)*x_{1}(t)=x_{1}(t)\,$

$x_{1}(t)*\delta (t-t_{o})=\delta (t-t_{o})*x_{1}(t-t_{o})=x_{1}(t-t_{o})\,$

Téoréma konvolusi

Lamun ${\mathcal {F}}\{x_{1}(t)\}\,$ atawa $X_{1}(\omega )$ ngalambangkeun transformasi Fourier tina fungsi $x_{1}(t)$, ${\mathcal {F}}\{x_{2}(t)\}\,$ atawa $X_{2}(\omega )$ ngalambangkeun transformasi Fourier tina fungsi $x_{2}(t)$, sarta $k$ hiji konstanta, mangka:

${\mathcal {F}}\{x_{1}(t)*x_{2}(t)\}=k\cdot {\mathcal {F}}\{x_{1}(t)\}\cdot {\mathcal {F}}\{x_{2}(t)\}=X_{1}(\omega )\cdot X_{2}(\omega )$

sarta:

$x_{1}(t)*x_{2}(t){\stackrel {\mathcal {F}}{\Longleftrightarrow }}\quad X_{1}(\omega )\cdot X_{2}(\omega )\,$

$x_{1}(t)\cdot x_{2}(t){\stackrel {\mathcal {F}}{\Longleftrightarrow }}\quad {\frac {1}{2\pi }}\cdot X_{1}(\omega )*X_{2}(\omega )\,$

Tempo ogé

• Toeplitz matrix (convolutions can be considered a Toeplitz matrix operation where éach row is a shifted copy of the convolution kernel)
  • Circulant matrix
• Cross-correlation
• Deconvolution
• Dirichlet convolution
• Titchmarsh convolution theorem
• Convolution power
• Analog signal processing
• List of convolutions of probability distributions

Tumbu kaluar

Tempo convolution dina Wikikamus, kamus bébas.

• http://www.nitte.ac.in/downloads/Conv-LTI.pdf Archived 2009-03-19 di Wayback Machine
• Convolution Archived 2006-02-21 di Wayback Machine, on The Data Analysis BriefBook
• http://www.jhu.edu/~signals/convolve/index.html Visual convolution Java Applet.
• http://www.jhu.edu/~signals/discreteconv2/index.html Visual convolution Java Applet for Discrete Time functions.
• Lectures on Image Processing: A collection of 18 lectures in pdf format from Vanderbilt University. Lecture 7 is on 2-D convolution., by Alan Peters.
  • http://www.vuse.vanderbilt.edu/~rap2/EECE253/EECE253_01_Intro.pdf Archived 2009-03-24 di Wayback Machine
• Convolution Kernel Mask Operation Interactive tutorial
• Convolution at MathWorld

Rujukan

1. Hsu, Hwei P., Schaum's Outline of Théory and Problems of Analog and Digital Communications, McGraw Hill, 1993