Médan Listrik
Médan listrik nyaéta éfék anu ditimbulkan ku ayana muatan listrik, saperti éléktron, ion, atawa proton, dina rohangan sabudeureunana. Médan listrik mibanda hijian N/C atawa dibaca newton/coulomb. Médan listrik umumna diajarkeun dina élmu fisika sarta widang-widang nu patali. Sacara teu langsung, widang éléktronika geus ngamangpaatkeun médan listrik nu aya dina kawat konduktor (kabel).
Asal médan listrik[édit | édit sumber]
Rumus matematika pikeun médan listrik bisa diturunkeun tina Hukum Coulomb, nyaéta nu ngarumuskeun gaya antara dua titik muatan:
.
Nurutkeun rumus ieu, gaya dina salah sahiji titik muatan babanding lempeng jeung gedé muatanana. Médan listrik didéfinisikeun minangka hiji konstanta babandingan antara muatan jeung gaya Andrew Duffy, Electric field, PY106/Electricfield.html, 7-7-99.:
Mangka, médan listrik gumantung kana patempatan (posisi).
Hiji médan, mangrupa hiji véktor anu gumantung kana véktor séjénna. Medan listrik bisa dianggap salaku gradién tina poténsial listrik. Lamun sawatara muatan anu disebarkeun ngahasilkeun poténsial listrik, gradién poténsial listrik bisa ditangtukeun.
Konstanta k[édit | édit sumber]
Dina rumus listrik mindeng dipanggihan konstanta k salaku gaganti ti (dina tulisan ieu tetep dipaké anu pamungkas), di mana konstanta kasebut boga harga Reference Tables for Physical setting/Physics, 2002 Edition, The University of The State of New York, 2002.:
anu mindeng disebut konstanta kasataraan gaya listrik J.S. Covacs, Coulomb's Law, Physnet, MISN-0-114, hal 3.
Ngitung médan listrik[édit | édit sumber]

Pikeun ngitung médan listrik dina hiji titik alatan ayana hiji titik muatan anu perenahna dina dipaké rumus:
- vektor (kalawan panah di luhurna), sarta
- vektor (dicitak kandel).
Tempo: Vector Notation, vec-not-prae, revised 6/02.
Panyederhanaan anu kurang pas[édit | édit sumber]
Umumna pikeun ngalakonan panyederhanaan dipilih puseur koordinat silih hapit jeung titik muatan anu perenahna dina sahingga dihasilkeun rumus jiga nu dituliskeun dina awal artikel ieu, atawa lamun dituliskeun balik dina notasi vektornya:
kalawan vektor hijian
.
Disarankeun pikeun ngagunakeun rumusan anu ngalibetkeun sarta alatan leuwih umum, sarta bisa dilarapkeun pikeun kasus nu ngandung muatan leuwih ti hiji sarta ogé dina distribusi muatan, boh distribusi diskrit boh kontinu. Panyederhanaan ieu ogé sakapeung ngajadikeun pamahaman dina ngitung médan listrik jadi saeutik rada teu jelas. Sajaba ti éta ogé lantaran panyederhanaan ieu ngan mangrupa salah sahiji kasus husus dina itungan médan listrik (kasus ku hiji titik muatan di mana titik muatan ditempatkeun di puseur koordinat).
Tanda muatan listrik[édit | édit sumber]

Muatan listrik bisa boga harga négatif, enol (heneuweuh muatan atawa jumlah hijian muatan positif jeung négatif sarua) sarta négatif. Harga muatan ieu baris mangaruhan itungan médan listrik dina hal tandana, nyaéta positif atawa négatif (atawa enol). Lamun dina saban titik di sabudeureun hiji muatan (atawa leuwih) diitung medan listrikna sarta digambarkeun vektor-vektorna, mangka baris katémbong garis-garis anu silih sambung, anu disebut sabagé garis-garis médan listrik. Tanda muatan nangtukeun naha garis-garis médan listrik anu dihasilkeun téh asalna tina éta muatan atawa nuju ka éta muatan. Geus ditangtukeun (dumasar kana gaya anu dirandapan ku muatan uji positif), yén
- muatan positif (+) baris ngabalukarkeun garis-garis médan listrik arahna ti muata nuju kaluar,
- muatan négatif (-) baris ngabalukarkeun garis-garis médan listrik arahna asup nuju ka muatan.
- muatan enol ( ) henteu ngabalukarkeun ayana garis-garis médan listrik.
Gradién poténsial listrik[édit | édit sumber]
Médan listrik bisa ogé diitung lamun hiji poténsial listrik dipikanyaho, ngaliwatan itungan gradiénna Carl R. Nave, Electric Field as Gradient, Hyperphysics, electric/efromv.html#c2, 2006.:
di mana
pikeun sistem koordinat kartésian.
Énergi médan listrik[édit | édit sumber]
Médan listrik nyimpen énergi. Rapet énergi hiji médan listrik dijelaskeun ku David Land, Electrostatic field energy, ELMAG305/em8a/sld006.htm Archived 2006-08-21 di Wayback Machine, 18.10.1999 17:05:51.
kalawan
- nyaéta permitivitas médium di mana médan listrik nyondong, dina rohangan hapa .
- nyaéta véktor médan listrik.
Total énérgi anu kasimpen dina médan listrik dina hiji volume nyaéta
di mana
- nyaéta élemen diferensial volume.
Distribusi muatan listrik[édit | édit sumber]
Médan listrik henteu waé ngan ditimbulkan ku hiji muatan listrik, tapi ogé bisa ditimbulkan ku leuwih ti hiji muatan listrik, malah ku distribusi muatan listrik boh anu diskrit boh anu kontinu. Conto-conto distribusi muatan listrik nyaéta:
- kumpulan titik-titik muatan
- kawat panjang lempeng nu boga tungtung sarta nu teu-boga tungtung
- bunderan kawat
- pelat rubak boga tungtung atawa teu-boga tungtung
- cakra ipis sarta lélépén
- wangun-wangun séjén
Kumpulan titik-titik muatan[édit | édit sumber]
Pikeun titik-titik muatan anu sumebar sarta jumlahna henteu réa teuing, médan listrik dina sahiji titik (lain dina salah hiji titik muatan) bisa diitung ku cara ngajumlahkeun véktor médan listrik dina titik-titik kasebut akibat unggal muatan. Dina kasus ieu leuwih alus dituliskeun
anu dibaca, médan listrik di titik \vec{r} akibat ayana muatan \! q_i anu perenahna dina \vec{r}_i. Ku kituna médan listrik di titik \vec{r} akibat sakabéh muatan anu sumebar dituliskeun sabagé
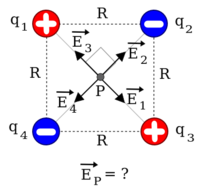
di mana nyaéta jumlah titik muatan. Minangka gambaran, contona lamun urang hayang nangtukeun gedéna médan listrik dina titik \!P anu mangrupa patimuan dua diagonal hiji bujursangkar nu boga sisi , di mana aya ku opat muatan titik anu perenahna dina kaoptat titik sudut bujursangkar kasebut. Pikeun kasus ieu misalkeun yén sarta sarta cokot puseur koordinat di titik pikeun ngagampangkeun. Pikeun kasus dua diménsi kawas ieu, bisa dituliskeun ogé
anu baris ngahasilkeun
ku kituna
anu ngahasilkeun yén médan listrik dina titik kasebut nyaéta enol.
Kawat panjang lempeng[édit | édit sumber]
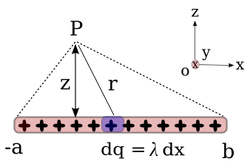
Kawat panjang lempeng mangrupa salah sahiji wangun distribusi muatan anu narik ati lantaran lamun panjangna diupamakeun teu-boga tungtung, itungan muatan dina hiji jarak ti kawat jeung perenahna di tengah-tengah badan kawat, jadi kacida gampang.
Pikeun hiji kawat anu lempeng dina sumbu , dina jarak di luhurna, sarta kawat manteng ti nepi ka ti titik proyeksi dina kawat, médan listrik di titik kasebut bisa diitung gedéna, nyaéta:
Saperti nu geus disebutkeun di luhur, lamun jeung mangka kalawan ngagunakeun dalil L'Hospital dihasilkeun
Atawa lamun kawat nu ditempatkeun sajajar jeung sumbu-z sarta widang x-y ditembus kawat sacara ajeg lempeng, mangka médan listrik di hiji titik nu jarakna ti kawat, médan listrikna nyaéta
di mana nyaéta véktor hijian radial dina koordinat silinder:
di mana nyaéta sudut anu dijieun ku sumbu-x positif.



















































![{\displaystyle E_{z}={\frac {1}{4\pi \epsilon _{0}}}{\frac {\lambda }{z}}\left[{\frac {b}{\sqrt {z^{2}+b^{2}}}}+{\frac {a}{\sqrt {z^{2}+a^{2}}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5e3f2a31ee7d283e4c058bf9793db35a34b70f2)







