Sebaran-t student
Dina kamungkinan jeung statistik, sebaran-t atawa sebaran Student loba digunakeun keur nga-estimasi mean tina populasi nu kasebar sacara normal dina waktu ukuran sampelna leutik. Dasar nu kawentar Student's t-test nyaéta keur statistical significance tina dua sampel mean anu béda, sarta interval kapercayaan keur dua populasi méans anu béda.
Asal tiori ngeunaan sebaran-t mimiti dipublikasi dina taun 1908 ku William Sealey Gosset dina paper nu ditulis pseudonym Student. Tiori Tes-t sarta hal nu pakait leuwih dipikaharti dina tulisan-tulisan R.A. Fisher, nu nyebut ieu sebaran ku "Student's distribution".
Student's distribution loba digunakeun lamun (saperti digunakeun dina statistik praktis) populasi simpangan baku teu dipikanyaho sarta bakal di-estimasi tina data. Dina buku teksbook dijelaskeun yén simpangan baku lamun dipikanyaho aya dua tipe nyaet: (1) dina hal ukuran sampel kacida gedéna yén salah sahiji keur nganyahokeun simpangan baku tina data ku cara nga-estimasi varian lamun varian pasti, jeung (2) keur ngagambarkeun alesan sacara matematik, nu mana masalah estimasi simpangan baku kadangkadal "diabaikan" sabab lain mangrupa hal anu kudu dijelaskeun ku pangarang atawa instruktur.
Kumaha sebaran-t student loba dipake
[édit | édit sumber]Anggap X1, ..., Xn mangrupa variabel acak bebas nu kasebar normal mibanda nilai harepan μ sarta varian σ2. Saterusna
dijadikeun "sample mean", sarta
dijadikeun "sample variance". Saperti anu ditempo di handap ieu
mangrupa sebaran normal nu mibanda méan 0 sarta variance 1. Gosset nalungtik hubungan kualitas jadi,
sarta nembongkeun yén T mibanda fungsi dénsitas probabilitas
nu mana ν sarua jeung n − 1. Sebaran T éta ayeuna disebut sebaran-t. Paraméter ν sacara konvensional disebut angka degrees of freedom atawa tingkat kabébasan. Sebaran gumantung kana nilai ν, lain kana nilai μ atawa σ; heunteu gumantungna ieu sebaran kana nilai μ jeung σ ngajadikeun sebaran-t-penting boh dina tiori sarta prakték.
Kumaha cara make sebaran t-student
[édit | édit sumber]Interval dina titik ahir nyaéta
nu mana A nyaéta pamarekantitik-persentasi sebaran -t, mangrupa interval kapercayaan keur μ. Saterusna, lamun nilai méan tina susunan observasi dipikanyaho maka bisa disebutkeun aya alesan keur merkirakeun yén data ngaboogan sebaran normal, bisa digunakeun sebaran-t keur nge-tes confidence limits nu sacara tiori méan kaasup nilai nu diprediksi - saperti nilai prediksi dina null hypothesis.
Hasil ieu digunakeun dina Student's t-test: béda antara dua sampel méan tina dua sebaran normal bakal mibanda kasebar sacara normal, sebaran-t bisa digunakeun keur ngetes béda ieu nu sacara alesan statistik bisa diperkirakeun bakal jadi nol.
Angka statistik séjén nunjukkeun yén sebaran-t keur sampel anu ukuran sedeng aya dina kaayaan null hypothesis nu dipiharep, sabab kitu bentuk sebaran-t jadi dasar keur tes signifikan di kaayaan séjén nu sarua hadéna waktu ngetes béda dua méan. Contona, sebaran Spearman's rank correlation coefficient, rho, dina kasus null (taya korelasi) nembongkeun hasil nu hadé ku pamarekansebaran-t keur ukuran sample leuweih ti 20.
Tempo prediction interval keur conto séjén nu maké distribusi ieu.
Tiori lanjutan
[édit | édit sumber]Hasil Gosset's bisa netepkeun hal nu leuwih umum. (Keur conto tempo Hogg and Craig, Bagéan 4.4 and 4.8.) Anggap Z mibanda sebaran normal nu mibanda méan 0 sarta variance 1. Anggap V mibanda sebaran chi-kuadrat nu mibanda ν tingkat kabébasan. Terus kira-kira yén Z sarta V mangrupa bebas (tempo teorema Cochran). Mangka rasio
mibanda sebaran-t nu mibanda ν tingkat kabébasan.
Keur sebaran-t nu mibanda ν tingkat kabébasan, nilai ekspektasi 0, sarta varian ν/(ν − 2) lamun ν > 2. Skewness na 0 sarta kurtosis na 6/(ν − 4) lamun ν > 4.
Fungsi sebaran kumulatif dijelaskeun dina fungsi béta teu lengkep,
nu mibanda
Sebaran-t aya hubunganna jeung sebaran-F nyaéta: nilai kuadrat t nu mibanda ν tingkat kabébasan disebarkeun salaku F nu mibanda nilai 1 sarta ν tingkat kabébasan.
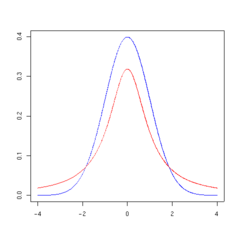
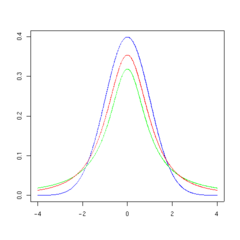
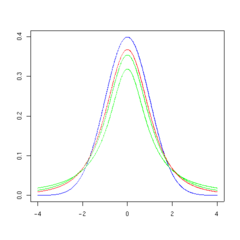
Sakabéh fungsi probability density sebaran-t digambarkeun dina bentuk bel salaku variabel sebaran normal nu mibanda nilai méan 0 sarta varian 1, iwal ti mibanda nilai nu leuwih handap sarta ngalegaan bentuk belna. Salaku jumlah tingkat kabébasan anu nambahan, sebaran-t ngadeukeutan sebaran normal nu mibanda nilai méan 0 sarta varian 1.
Gambar di handap ieu nunjukkeun densitas sebaran-t dina kaayaan beuki naekna nilai ν. Sebaran normal ditempokeun dina garis biru keur perbandingan. Catetan yén sebaran-t (garis beureum) jadi rapet jeung sebaran normal lamun ν ogé ningkat. Keur ν = 30 sebaran-t persis sarua jeung sebaran normal.
 |  |  |
 |  |  |
Sumber sejen
[édit | édit sumber]- "Student" (W.S. Gosset) (1908) The probable error of a méan. Biometrika 6(1):1--25.
- M. Abramowitz and I. A. Stegun, eds. (1972) Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover. (See Section 26.7.)
- R.V. Hogg and A.T. Craig (1978) Introduction to Mathematical Statistics. New York: Macmillan.
Tumbu kaluar
[édit | édit sumber]- Earliest Known Uses of Some of the Words of Mathematics (S) (Remarks on the history of the term "Student's distribution")









